Распределение температуры в области D в стационарном случае при отсутствии притока тепла во внутренних точках области удовлетворяет однородному уравнению Лапласа:

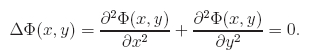
Очевидно, что решение стационарной задачи не зависит от коэффциента теплопроводности.

Одним из подходов к решению стационарного уравнения теплопрводности является так называемый метод установления. В этом случае решается нестационарное уравнение теплопроводности с некоторым начальным распределением температуры и стационарными грничными условиями. В решении время устремляется к бесконечнсти, когда решение "устанавливается", то есть перестает меняться с течением времени. Это решение совпадает с решением стационарного уравнения.

Нестационарное уравнение теплопроводности имеет вид

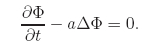
Коэффициент α теплопроводности влияет только на скорость устновления решения, поэтому положим его равным единице.

Не вдаваясь в теорию численных методов (подробности вы можете найти в соответствующей литературе), запишем разностное представление решения этого уравнения.

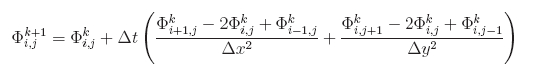
Здесь Δt - шаг по времени, Δx и Δy - шаги по пространственным координатам X и Y соответственно. Индексы k,i и j - индексы по времени и координатам X и Y соответственно.

В качестве области вычислений мы для простоты берем прямоугольную сетку, значения на границе которой мы задаем некоей функцией

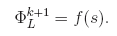
Для нахождения решения этого уравнения мы проводим последовательные итерации на сетке, а в качестве критерия установления решения используем критерий

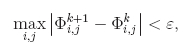
где ε - заданное малое положительное число.

При выполнении расчетов необходимо провести исследование устойчивости нашей разностной схемы, а именно проверить условие сходимости:

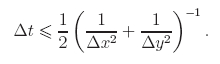
В следующей главе мы для начала рассмотрим обычную последовательную программу, реализующую решение этого уравнения.