Предыдущая статья дает слишком пессимистические прогнозы по оценке эффективности кластера. Пессимизм заложен в формуле №2 статьи, которая в сущности описывает как сетевую инфраструктуру кластера, так и способ разделения исходной разностной сетки между узлами кластера. В данной работе мы попробуем изменить подход к этим вопросам на более реалистичный.

В статье оценка времени граничного объема записана так:

(1)

где E – объем данных в области граничного обмена (Гбит), V – пропускная способность сети кластера (Гбит/с). В ней используется скорость порта в единицах Гбит/с. Далее будем обозначать его как V_p. В действительности все немного сложнее.

Есть очень интересный момент. Современные коммутаторы имеют такую характеристику, как «пропускная способность шины». Например 8-портовый коммутатор SuperStack II Switch 9000 имеет пропускную способность 17.2 Гбит/с. Это означает, что каждый из восьми портов может одновременно с другими в дуплексном режиме передавать и принимать данные с суммарной скоростью 2 Гбит/с. Точнее говоря, пропускная способность шины задана в пакетах в секунду и заявленные 17.2 Гбит/с достигается при пересылке больших пакетов данных. Но будем считать, что наши граничные области именно такие.

Таким образом, узел передает данные не быстрее, чем позволяет порт, а с другой стороны, суммарная скорость передаваемых и принимаемых всеми узлами данных не может превышать пропускной способности коммутатора (далее будем обозначать ее как V_b).

Поэтому, в предположении, что все узлы инициируют обмен данными одновременно (в том числе одновременно и передачу и прием), исходную формулу расчета времени обмена в условиях дуплексного режима работы сетевых интерфейсов следует записать таким образом:

для (2)

и

для (3)

Здесь E_i - количество ячеек разностной сетки типа real*8 отдельно взятого узла, участвующих в граничном обмене. Если мы распределяем исходную разностную сетку между узлами, деля ее равномерно по одной координате, то это величина постоянная.

Поскольку время одной итерации вычислительного процесса складывается из двух величин – времени непосредственно счета и времени обмена данными между узлами кластера

(4),

то следует ожидать, что эффективная скорость счета кластера будет расти примерно до момента, когда

(5)

Таким образом мы можем оценить количество узлов кластера, при котором задача будет решаться наиболее эффективно. На тестовом компьютере (Intel Pentium 4 3GHz), имеющемся в моем распоряжении скорость расчетов задачи Эйлера при использовании компилятора Intel Fortran Compiler составляет примерно 0.87 секунды на одну итерацию для разностной сетки размером 6000х6000 элементов типа real*8. То есть скорость вычислений равна примерно 2600 Мбит/сек. (2.6·10⁹ бит/сек.) для одной итерации. Если эту скорость вычислений обозначить как V_c, то время одной итерации можно записать как

(6)

Здесь E_n - количество элементов разностной сетки размерности real*8 (64 бита), которое обрабатывается узлом кластера. Параметр V_c зависит не только от мощности центрального процессора, но может различаться в различных задачах, поскольку в нем заложена «мощность вычислений», то есть количество математических операций, требующихся для обработки одной ячейки разностной сетки.

Будем считать, что целью распараллеливания программы является уменьшение общего времени счета, а не увеличение доступной для расчетов памяти, то есть общий размер разностной сетки не зависит от числа улов кластера. Следовательно, учитывая соотношение (5), оптимальное количество узлов кластера можно оценить по формуле

для (7)

и

для (8)

Если считать, что деление сетки между узлами происходит только по одной координате и распределение по узлам выполняется равномерно, то объем данных (количество обрабатываемых ячеек сетки) области вычислений для каждого узла будет равен

(9)

Здесь E_x - длина разностной сетки по оси X, а E_i - как и раньше длина массива граничной области и одновременно длина разностной сетки по оси Y. Таким образом из уравнений (7), (8) и (9) мы получаем два условия:

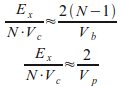(10)

Отсюда мы получаем два значения оптимального количества узлов кластера при котором общее время вычислений, требуемое для решения задачи будет минимальным:

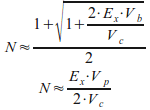(11)

Первое значение, полученное по теореме Виета, применимо при условии V_b≤V_p·N, а второе - при условии V_b>V_p·N.

Для иллюстрации вышесказанного попробуем рассмотреть поведение некоего абстрактного кластера при решении задачи Эйлера. Для эксперимента зададим начальные условия:

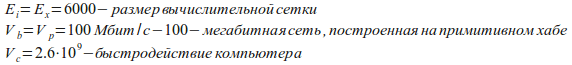
Применив соотношение (11) мы получим значения N равные 11 и 115 соответственно. Но, поскольку значение 115 явно не удовлетворяет условию V_b>V_p·N, то считаем, что оптимальный размер кластера для нашей задачи составляет 11 узлов. При таком размере кластера наша задача будет считаться примерно в 6 раз быстрее, чем если бы она была посчитана на одной машине.

В качестве проверки наших рассуждений попробуем построить график функции (4) при указанных условиях эксперимента.

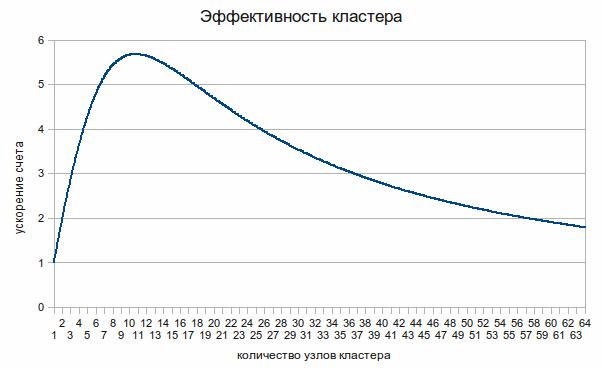Рис. 1

Теперь вернемся к формуле (11). Результат получился на первый взгляд достаточно парадоксальным, а именно: оптимальное количество узлов кластера не зависит от размера области обмена. Однако, как было упомянуто выше, распределение вычислительной области между узлами кластера осуществлялось таким образом, что размер области обмена оставался постоянным, так что, соотношение времени, потраченного на обработку этой области и времени ее пересылки так же оставалось постоянным, не зависящим от ее размера.

Второй вывод, который можно сделать, заключается в следующем. Оптимальное количество узлов кластера (дающее наибольшее быстродействие) уменьшается с увеличением вычислительной мощности компьютеров, из которых состоит кластер. Но это вполне понятно, поскольку сетевой обмен между узлами кластера будет тем заметнее тормозить общий вычислительный процесс, чем меньше времени будет тратиться непосредственно на вычисления.

Наконец перейдем к более реальному случаю. Как и было сказано в самом начале, предыдущая статья дает слишком пессимистический прогноз эффективности кластера. Следуя формуле (11) Можно предположить, что при использовании современных коммутаторов и увеличении объема вычислений можно ожидать существенного роста эффективности работы параллельной программы. Для проверки этого предположения возьмем процессор Intel E8400 3 GHz, который дает скорость V_c≈1.4·10¹⁰ и задачу Эйлера с общим объемом разностной сетки порядка 4 Гб. Сеть кластера построим на упомянутых выше маршрутизаторах SuperStack II Switch 9000.

Таким образом имеем начальные условия:

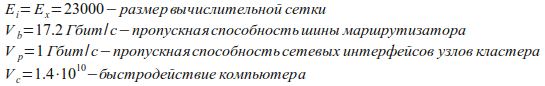
Оценочный размер максимально эффективного кластера согласно формуле (11) будет равен 119 узлов. А время счета по сравнению с одно-процессорным вариантом уменьшится примерно в 60 раз. Причем, если построить график, аналогичный рис. 1, то можно увидеть, что эффективность кластера до размера в несколько десятков узлов растет примерно линейно.

Теперь рассмотрим один нюанс, касающийся высокопроизводительных вычислений с использованием кластерной архитектуры, хотя к кластерам, как таковым, этот нюанс отношения не имеет. Речь пойдет о стиле программирования. Очень часто забывают, что на скорость вычислений влияет не только выбранный алгоритм, который затем реализуется в программный код, но и особенности компилятора в совокупности с реализацией механизмов доступа к оперативной памяти.

Подробно описывать эти особенности я не буду — все это можно найти в специальной литературе. В двух же словах проблема, с которой может столкнуться программист, заключается в том, что в современных компьютерах доступ к ячейкам оперативной памяти организован так, то последовательный доступ к соседним ячейкам выполняется гораздо быстрее, нежели чем последовательный доступ к ячейкам, разделенным большими промежутками.

В данной работе в качестве тестового примера была взята задача Эйлера. Разностное представление решения этой задачи выгладит следующим образом:

Соответственно этому имеем такой программный код на языке Fortran: 

      do x=2,xmax-1 

        do y=2,ymax-1 

        f1(x,y)=f0(x,y)+dt*( 

     x    (f0(x+1,y)-2*f0(x,y)+f0(x-1,y))/(dx*dx) 

     x    + 

     x    (f0(x,y+1)-2*f0(x,y)+f0(x,y-1))/(dy*dy) 

     x    ) 

        end do 

      end do

Казалось бы все правильно. С точки зрения математики так и есть. Однако попытка экспериментально определить скорость обработки данных этой программой при различных размерах разностной сетки дает вот такие странные результаты:

Размер сетки	Vc, Мбит/сек.	Размер сетки	Vc, Мбит/сек.
600x600	1963	3000x3000	591
1000x1000	1967	6000x3000	420
1000x3000	732	3000x6000	285
3000x3000	1841	6000x6000	242

Теперь немного изменим текст программы, изменив вложенность циклов:

      do y=2,ymax-1 

        do x=2,xmax-1 

        f1(x,y)=f0(x,y)+dt*( 

     x    (f0(x+1,y)-2*f0(x,y)+f0(x-1,y))/(dx*dx) 

     x    + 

     x    (f0(x,y+1)-2*f0(x,y)+f0(x,y-1))/(dy*dy) 

     x    ) 

        end do 

      end do

Ни с точки зрения математики, ни с точки зрения полученных результатов решения задачи ничего не изменилось. Однако теперь эксперимент показывает радикальное изменение скорости обработки данных. Смотрим таблицу.

Размер сетки	Vc, Мбит/сек.	Размер сетки	Vc, Мбит/сек.
600x600	2618	3000x3000	2643
1000x1000	2637	6000x3000	2644
1000x3000	2622	3000x6000	2647
3000x3000	2627	6000x6000	2643

Таким образом, установка правильной последовательности обращения к ячейкам разностной сетки (и соответственно к ячейкам оперативной памяти компьютера) дает возможность не только стабилизировать скорость выполнения программы, убрав зависимость от размеров и конфигурации области счета, но и существенно ее (скорость) увеличить.